7.10 Problem Challenge 2 - Right View of a Binary Tree (easy)

Given the root of a binary tree, imagine yourself standing on the right side of it, return the values of the nodes you can see ordered from top to bottom.

Example 1:

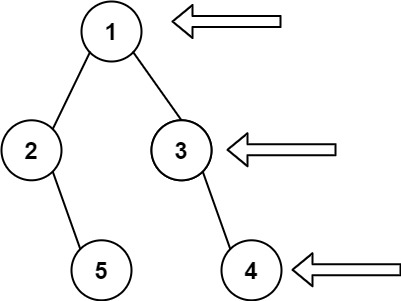
Input: root = [1,2,3,null,5,null,4]
Output: [1,3,4]

Example 2:

Input: root = [1,null,3]
Output: [1,3]

Example 3:

Input: root = []
Output: []

Constraints:

• The number of nodes in the tree is in the range [0, 100].

• -100 <= Node.val <= 100

import java.util.*;

class TreeNode {
  int val;
  TreeNode left;
  TreeNode right;

  TreeNode(int x) {
    val = x;
  }
};

class Main {
  public static List<TreeNode> traverse(TreeNode root) {
    List<TreeNode> result = new ArrayList<>();
      if(root == null) return result;
        
      Queue<TreeNode> q = new LinkedList<>();
      q.offer(root);
        
      while(!q.isEmpty()) {
        int levelSize = q.size();
          // List<TreeNode> currLevel = new ArrayList<>();
          for(int i = 0; i < levelSize; i++) {
            TreeNode curr = q.poll();
            // currLevel.add(curr);
            if(i == levelSize-1)
              result.add(curr);
                
            if(curr.left != null) q.offer(curr.left);
            if(curr.right != null) q.offer(curr.right);
          }
            
          // result.add(currLevel.get(currLevel.size()-1));
      }
    
    return result;
  }

  public static void main(String[] args) {
    TreeNode root = new TreeNode(12);
    root.left = new TreeNode(7);
    root.right = new TreeNode(1);
    root.left.left = new TreeNode(9);
    root.right.left = new TreeNode(10);
    root.right.right = new TreeNode(5);
    root.left.left.left = new TreeNode(3);
    List<TreeNode> result = Main.traverse(root);
    for (TreeNode node : result) {
      System.out.print(node.val + " ");
    }
  }
}

Time complexity #

The time complexity of the above algorithm is O(N), where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once.

Space complexity #

The space complexity of the above algorithm will be O(N), which is required for the queue. Since we can have a maximum of N/2 nodes at any level (this could happen only at the lowest level), therefore we will need O(N) space to store them in the queue.