7.6 Maximum Depth of Binary Tree (easy)

Given the root of a binary tree, return its maximum depth.

A binary tree's maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Example 1:

Input: root = [3,9,20,null,null,15,7]
Output: 3

Example 2:

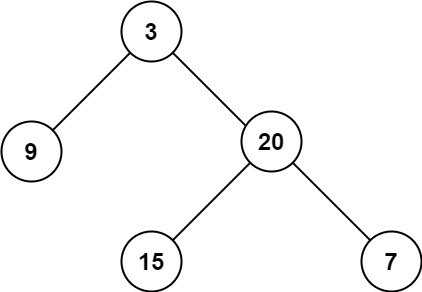
Input: root = [1,null,2]
Output: 2

Constraints:

• The number of nodes in the tree is in the range [0, 104].

• -100 <= Node.val <= 100

import java.util.*;

class TreeNode {
  int val;
  TreeNode left;
  TreeNode right;

  TreeNode(int x) {
    val = x;
  }
};

class Main {
  public static int findDepth(TreeNode root) {
    if (root == null)
      return 0;
    Queue<TreeNode> queue = new LinkedList<>();
    int maximumTreeDepth = 0;
    queue.offer(root);

    while(!queue.isEmpty()) {
      maximumTreeDepth++;
      int levelSize = queue.size();
      for(int i = 0; i < levelSize; i++) {
        TreeNode currNode = queue.poll();
        if(currNode.left != null) queue.offer(currNode.left);
        if(currNode.right != null) queue.offer(currNode.right);
      }
    }


    return maximumTreeDepth;
  }

  public static void main(String[] args) {
    TreeNode root = new TreeNode(12);
    root.left = new TreeNode(7);
    root.right = new TreeNode(1);
    root.right.left = new TreeNode(10);
    root.right.right = new TreeNode(5);
    System.out.println("Tree Maximum Depth: " + Main.findDepth(root));
    root.left.left = new TreeNode(9);
    root.right.left.left = new TreeNode(11);
    System.out.println("Tree Maximum Depth: " + Main.findDepth(root));
  }
}

Time complexity #

The time complexity of the above algorithm is O(N), where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once.

Space complexity #

The space complexity of the above algorithm will be O(N) which is required for the queue. Since we can have a maximum of N/2 nodes at any level (this could happen only at the lowest level), therefore we will need O(N) space to store them in the queue